- PORTADA
- SINTESIS
- AREA DE UN CIRCULO
- AREA DE UN CUADRADO
- AREA DE UN HEXAGONO
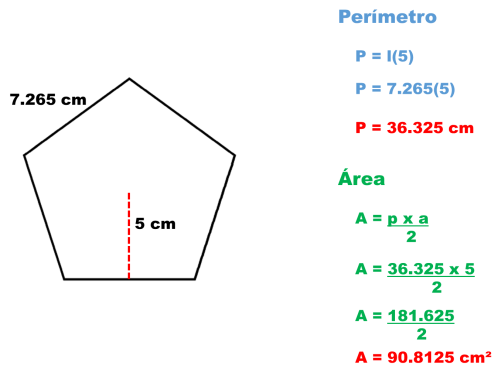
- AREA DE UN PENTAGONO
- AREA DE UN OVALO
- AREA DE UN TRAPECIO
- AREA DE UN ROMBO
- AREA DE UN RECTANGULO
- AREA DE UN ROMBOIDE
- AREA DE UN TRIANGULO ESCALENO
- AREA DE UN TRIANGULO EQUILATERO
- AREA DE UN TRIANGULO ISOSCELES
- JUEGA Y APRENDE
- JUEGA Y APRENDE
- JUEGA Y APRENDE
- POWER POINT
- EXCEL
- GOOGLE FORMS
jueves, 14 de junio de 2018
INDICE
PORTADA
COLEGIO DE BACHILLERES: "COBAY CHENKU"
TEMA: ÁREAS DE FIGURAS PLANAS
INTEGRANTES:
CHRISTOPHER ALCOCER CANDILA
MELISSA LORIA POLANCO
LAURA CABALLERO CANUL
CRISTINA REYES BAAS
ANDREA CASTILLO VEGA
GRADO: 2 GRUPO: J
miércoles, 13 de junio de 2018
SINTESIS
ÁREA DE FIGURAS PLANAS
El área es un concepto métrico que permite asignar una medida a la extensión de una superficie, expresada en matemáticas como unidades de medida denominadas unidades de superficie. El área es un concepto métrico que requiere la especificación de una medida de longitud.
Para superficies planas, el concepto es más intuitivo. Cualquier superficie plana de lados rectos, es decir, cualquier polígono, puede triangularse, y se puede calcular su área como suma de las áreas de los triángulos en que se descompone. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).
Ahora ¿qué es la Geometría?
Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).
Es la base teórica de la geometría descriptiva o del dibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales).
Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada, mecánica, arquitectura, geografía, cartografía, astronomía, náutica, topografía, etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanía.
La necesidad de la enseñanza de la geometría es muy importante en la vida escolar, en primer lugar, al papel que la geometría desempeña en la vida cotidiana.
Un conocimiento geométrico básico es indispensable para desenvolverse en la vida cotidiana: para orientarse reflexivamente en el espacio; para hacer estimaciones sobre formas y distancias; para hacer apreciaciones y cálculos relativos a la distribución de los objetos en el espacio, etc.
La geometría está presente en múltiples ámbitos del sistema productivo de nuestras actuales sociedades (producción industrial, diseño, arquitectura, topografía, etc…).
De esto la geometría tiene su importancia en la vida y casi en todos lados, generalmente no se aprende en el jardín de niños sino hasta el octavo grado, pero los niños comienzan a aprender figuras y espacios en diferentes maneras. En actividades escolares iniciales los estudiantes del jardín de niños deben colorear triángulos y círculos. Al final de la escuela primaria la mayoría de los estudiantes son capaces de hacer dibujos a escala.
Y con esto del mundo actual del avance de la tecnología, también se aplica, como en gráficos o en diseño, uno de los ejemplos serían como: los diseños de ingeniería estructural para edificios primero se generan por computadora. El modelado de proteínas involucra el uso de la geometría para replicar las imágenes de las proteínas. Los científicos diseñan medicamentos para cambiar la forma o movimiento de las proteínas y así curar enfermedades. En la medicina la forma de un tumor se reconstruye mediante un escaneo de TAC. Etc.
En resumen la geometría esta en todas partes: edificios, aviones, automóviles y mapas. Las casas están hechas de estructuras geométricas básicas. Algunos rascacielos tienen ventanas hechas de rectángulos y cuadrados. Las grandes pirámides de Egipto están hechas de figuras geométricas. Muchas cosas o tal vez todo.
Ademas la geometría tiene su ventaja de ser una ciencia muy importante, porque todo se puede representar mediante figuras. Estudiando la esta ciencia, fácilmente puedes resolver problemas planteándolos en formas de figuras, como por ejemplo hay edificios modernos que se hacen con formas de figuras, entonces tubo que haber cálculos geométricos para elaborar esa construcción.
En realidad por ser rama de la matemática, esta área es muy útil para todo, y a servido para crear innovaciones que revolucionaron la vida en el planeta, como las antenas parabólicas que vienen de un principio geométrico de la parábola como lugar geométrico, las lamparas también vienen de la geometría. Y muchas cosas mas que se podrán innovar mediante esta ciencia.
En realidad por ser rama de la matemática, esta área es muy útil para todo, y a servido para crear innovaciones que revolucionaron la vida en el planeta, como las antenas parabólicas que vienen de un principio geométrico de la parábola como lugar geométrico, las lamparas también vienen de la geometría. Y muchas cosas mas que se podrán innovar mediante esta ciencia.
Y básicamente no tiene una desventaja o ninguna de hecho.
Mi conclusión es que la geometría es una de las ciencias mas importantes en el campo de medición de unidades, una ciencia que se estudia desde que nacemos, y gracias a esta ciencia que está relacionada con el dibujo y la arquitectura se han podido hacer obras o dibujos a tamaño escala o real, por medio de puntos y lineas, como la Torre Eiffel, o los pilares de Grecia, o la enorme iglesia de España, El Templo Expiatorio de la Sagrada Familia, conocido simplemente como la Sagrada Familia, es una basílica católica de Barcelona, diseñada por el arquitecto Antoni Gaudí. Iniciada en 1882, todavía está en construcción.
Esta ciencia es un gran campo trabajo para la expresión personal o el estudio de formas abstractas.
martes, 12 de junio de 2018
ÁREA DE UN CÍRCULO
Un círculo es el conjunto de todos los puntos en un plano a una distancia dada (llamado el radio ) desde un punto dado (llamado el centro.)
Un segmento de recta que conecta dos puntos en el círculo y pasa a través del centro es llamado un diámetro del círculo.
Un segmento de recta que conecta dos puntos en el círculo y pasa a través del centro es llamado un diámetro del círculo.
Claramente, si d representa la longitud de un diámetro y r representa la longitud de un radio, entonces d = 2 r .
El área de un círculo esta dada por la fórmula
A = π r 2 .
ÁREA DE UN CUADRADO
El área del cuadrado es igual a lado por lado.



Ejercicio
Calcular el área de un cuadrado de 5 cm de lado.

A = 52 = 25 cm2
ÁREA DE UN HEXÁGONO
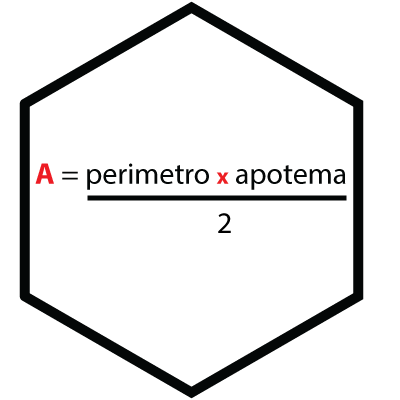
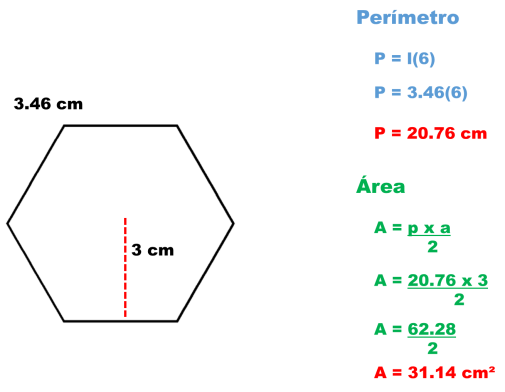
Un hexágono es un polígono que tiene seis lados y ángulos. Los hexágonos regulares tienen seis lados y ángulos iguales, y se componen de seis triángulos equiláteros.
EJEMPLO:
Un hexágono regular de 3.46 cm de lado y 3 cm de apotema.
AREA DE UN OVALO
OVALO
Un óvalo es una forma geométrica que se parece a un círculo alargado. Otro nombre para un óvalo es "elipse". Puede que sea necesario encontrar el área de un óvalo en una tarea de escuela intermedia, escuela secundaria o la clase de matemáticas de la universidad. El área de un óvalo es la cantidad de espacio contenida dentro de la forma.

EJEMPLO:
Mida la longitud de la elipse de "A" a "B" y divida por 2. Esto se conoce como "radio 1".

Mida el ancho del óvalo a través de su punto central. El punto central será la mitad de la longitud, esta longitud es la comprendida entre el punto "A'" y "B'". Una vez que se mida la anchura, divide este valor por 2. Esto se conoce como "radio 2".

Multiplique la mitad de la anchura por la mitad de la longitud. Por ejemplo, si el largo es de 10 centímetros y el ancho es de 6 centímetros, tendría que multiplicar 5 por 3 para obtener 15 centímetros.

Multiplique la respuesta del Paso 3 por pi, que es 3,14. En éste ejemplo, tendría que multiplicar 15 por 3,14 para obtener una superficie de 47,1 centímetros al cuadrado, que será el área de la elipse.

Un óvalo es una forma geométrica que se parece a un círculo alargado. Otro nombre para un óvalo es "elipse". Puede que sea necesario encontrar el área de un óvalo en una tarea de escuela intermedia, escuela secundaria o la clase de matemáticas de la universidad. El área de un óvalo es la cantidad de espacio contenida dentro de la forma.

EJEMPLO:
Mida la longitud de la elipse de "A" a "B" y divida por 2. Esto se conoce como "radio 1".

Mida el ancho del óvalo a través de su punto central. El punto central será la mitad de la longitud, esta longitud es la comprendida entre el punto "A'" y "B'". Una vez que se mida la anchura, divide este valor por 2. Esto se conoce como "radio 2".

Multiplique la mitad de la anchura por la mitad de la longitud. Por ejemplo, si el largo es de 10 centímetros y el ancho es de 6 centímetros, tendría que multiplicar 5 por 3 para obtener 15 centímetros.

Multiplique la respuesta del Paso 3 por pi, que es 3,14. En éste ejemplo, tendría que multiplicar 15 por 3,14 para obtener una superficie de 47,1 centímetros al cuadrado, que será el área de la elipse.

ÁREA DE UN TRAPECIO
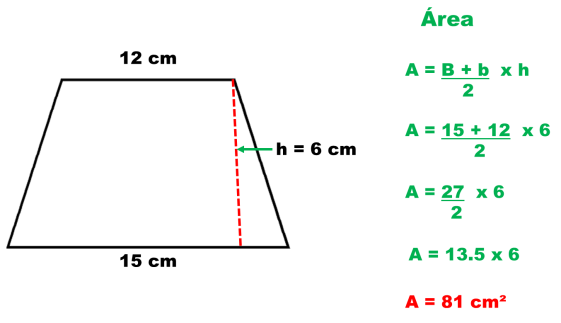
El área de un trapecio se calcula a partir de su altura y los dos lados paralelos (a y b) o bases del trapecio. Es el resultado de multiplicar su altura (h) y la mediana del trapecio, que se obtiene como la media de las dos bases a y b: M=(a+b)/2.
EJEMPLO:
Un trapecio cuyas bases miden 12 y 15 cm y de altura mide 6 cm
ÁREA DE UN ROMBO
Un rombo es un paralelogramo cuadrilátero con cuatro lados iguales.
Área:

Área:
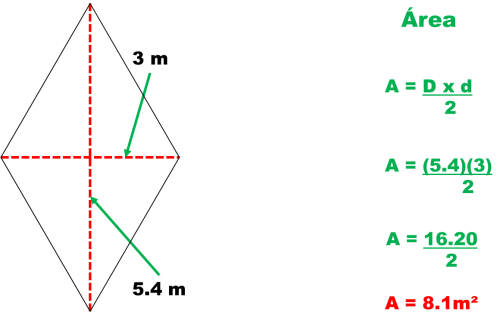
El área del rombo es igual al producto de diagonales dividido entre dos.
EJEMPLO:
Un rombo cuyas diagonales miden 5.4 cm y 3cm.
Con los datos conocidos puedo obtener el área.
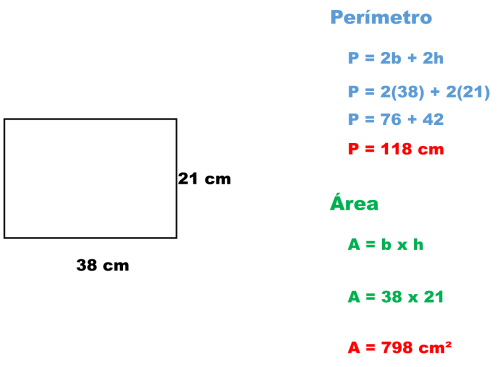
AREA DE UN RECTANGULO
Un rectángulo es un cuadrilátero con dos lados de igual longitud y dos lados de igual anchura que contiene cuatro ángulos rectos.
El rectángulo es un cuadrilátero, lo cual significa que tiene cuatro lados. Sus lados opuestos son iguales en longitud, así que los dos lados que marcan su longitud son iguales, y los que marcan su anchura son iguales también.
La ecuación para encontrar el área del rectángulo es simplemente A = h * b. Esto significa que el área de un rectángulo es igual al producto de su altura (h) por su base (b), o bien de su longitud por su anchura.
ÁREA DE UN ROMBOIDE
ROMBOIDE


El romboide es un paralelógramo (un tipo de cuadrilátero ) que no es ni rombo ni rectángulo ; es decir, un paralelógramo que tiene dos pares de lados paralelos e iguales entre sí (a = c; y b = d en la figura) formando dos pares de ángulos también iguales entre sí. (lados y ángulos iguales dos a dos).
A = a · h
En este caso, si tomamos como base el lado a.
EJEMPLO:
A = a . h
A = 5 · 3,5 = 17,5 cm2
domingo, 10 de junio de 2018
ÁREA DEL TRIÁNGULO ESCALENO
TRIÁNGULO ESCALENO
El triángulo escaleno es aquel que tiene todos los lados diferentes. Calcula fácilmente el área del triángulo escaleno con esta calculadora. La fórmula para calcular el área de un triángulo escaleno es siempre la misma: el área se obtiene siempre multiplicando la base por la altura y dividiendo el resultado por dos.


EJEMPLO:



El triángulo escaleno es aquel que tiene todos los lados diferentes. Calcula fácilmente el área del triángulo escaleno con esta calculadora. La fórmula para calcular el área de un triángulo escaleno es siempre la misma: el área se obtiene siempre multiplicando la base por la altura y dividiendo el resultado por dos.

EJEMPLO:
ÁREA DEL TRIÁNGULO EQUILÁTERO
TRIÁNGULO EQUILÁTERO
El triángulo equilátero es aquel que tiene todos los lados iguales. Calcula fácilmente el área del triángulo equilátero con esta calculadora. La fórmula para calcular el área de un triángulo equilátero es siempre la misma: el área se obtiene siempre multiplicando la base por la altura y dividiendo el resultado por dos.


EJEMPLO:


El triángulo equilátero es aquel que tiene todos los lados iguales. Calcula fácilmente el área del triángulo equilátero con esta calculadora. La fórmula para calcular el área de un triángulo equilátero es siempre la misma: el área se obtiene siempre multiplicando la base por la altura y dividiendo el resultado por dos.

EJEMPLO:
AREA DE TRIANGULO ISÓSCELES
TRIANGULOS ISÓSCELES
Un triángulo isósceles es un tipo de triángulo que tiene dos lados de igual longitud. A veces se especifica que tiene dos y solo dos lados de igual longitud y, a veces, que tiene al menos dos lados de igual longitud.

EJEMPLO:


Un triángulo isósceles es un tipo de triángulo que tiene dos lados de igual longitud. A veces se especifica que tiene dos y solo dos lados de igual longitud y, a veces, que tiene al menos dos lados de igual longitud.

EJEMPLO:
sábado, 9 de junio de 2018
juega y aprende
figuras planas
Crucigrama
Complete el crucigrama, luego haga clic en "Verificar" para verificar su respuesta. Si está atascado, puede hacer clic en "Sugerencia" para obtener una carta gratis. Haga clic en un número en la cuadrícula para ver la pista o pistas para ese número.
| 1 | ||||||||||
| 2 | ||||||||||
| 3 | 4 | |||||||||
| 5 |
|
|
||||||||||||||||
Suscribirse a:
Comentarios (Atom)